12.1 - Logistic Regression

Logistic regression models a relationship between predictor variables and a categorical response variable. For example, we could use logistic regression to model the relationship between various measurements of a manufactured specimen (such as dimensions and chemical composition) to predict if a crack greater than 10 mils will occur (a binary variable: either yes or no). Logistic regression helps us estimate a probability of falling into a certain level of the categorical response given a set of predictors. We can choose from three types of logistic regression, depending on the nature of the categorical response variable:

Binary Logistic Regression:

Used when the response is binary (i.e., it has two possible outcomes). The cracking example given above would utilize binary logistic regression. Other examples of binary responses could include passing or failing a test, responding yes or no on a survey, and having high or low blood pressure.

Nominal Logistic Regression:

Used when there are three or more categories with no natural ordering to the levels. Examples of nominal responses could include departments at a business (e.g., marketing, sales, HR), type of search engine used (e.g., Google, Yahoo!, MSN), and color (black, red, blue, orange).

Ordinal Logistic Regression:

Used when there are three or more categories with a natural ordering to the levels, but the ranking of the levels do not necessarily mean the intervals between them are equal. Examples of ordinal responses could be how students rate the effectiveness of a college course (e.g., good, medium, poor), levels of flavors for hot wings, and medical condition (e.g., good, stable, serious, critical).

Particular issues with modelling a categorical response variable include nonnormal error terms, nonconstant error variance, and constraints on the response function (i.e., the response is bounded between 0 and 1). We will investigate ways of dealing with these in the binary logistic regression setting here. Nominal and ordinal logistic regression are not considered in this course.

The multiple binary logistic regression model is the following:

where here \(\pi\) denotes a probability and not the irrational number 3.14.

• \(\pi\) is the probability that an observation is in a specified category of the binary Y variable, generally called the "success probability."
• Notice that the model describes the probability of an event happening as a function of X variables. For instance, it might provide estimates of the probability that an older person has heart disease.
• With the logistic model, estimates of $\pi$ from equations like the one above will always be between 0 and 1. The reasons are:
  • The numerator \(\exp(\beta_+\beta_X_+\ldots+\beta_X_)\) must be positive, because it is a power of a positive value (e).
  • The denominator of the model is (1 + numerator), so the answer will always be less than 1.

  For a sample of size n, the likelihood for a binary logistic regression is given by:

  This yields the log likelihood:

  Maximizing the likelihood (or log likelihood) has no closed-form solution, so a technique like iteratively reweighted least squares is used to find an estimate of the regression coefficients, $\hat$.

  

  To illustrate, consider data published on n = 27 leukemia patients. The data (leukemia_remission.txt) has a response variable of whether leukemia remission occurred (REMISS), which is given by a 1.

  The predictor variables are cellularity of the marrow clot section (CELL), smear differential percentage of blasts (SMEAR), percentage of absolute marrow leukemia cell infiltrate (INFIL), percentage labeling index of the bone marrow leukemia cells (LI), absolute number of blasts in the peripheral blood (BLAST), and the highest temperature prior to start of treatment (TEMP).

  The following output shows the estimated logistic regression equation and associated significance tests

  Coefficients
  Term Coef SE Coef 95% CI Z-Value P-Value VIF
  Constant 64.3 75.0 ( -82.7, 211.2) 0.86 0.391
  CELL 30.8 52.1 ( -71.4, 133.0) 0.59 0.554 62.46
  SMEAR 24.7 61.5 ( -95.9, 145.3) 0.40 0.688 434.42
  INFIL -25.0 65.3 (-152.9, 103.0) -0.38 0.702 471.10
  LI 4.36 2.66 ( -0.85, 9.57) 1.64 0.101 4.43
  BLAST -0.01 2.27 ( -4.45, 4.43) -0.01 0.996 4.18
  TEMP -100.2 77.8 (-252.6, 52.2) -1.29 0.198 3.01

  Wald Test

  The Wald test is the test of significance for individual regression coefficients in logistic regression (recall that we use t-tests in linear regression). For maximum likelihood estimates, the ratio

  can be used to test $H_: \beta_=0$. The standard normal curve is used to determine the $p$-value of the test. Furthermore, confidence intervals can be constructed as

  Estimates of the regression coefficients, $\hat$, are given in the Coefficients table in the column labeled "Coef." This table also gives coefficient p-values based on Wald tests. The index of the bone marrow leukemia cells (LI) has the smallest p-value and so appears to be closest to a significant predictor of remission occurring. After looking at various subsets of the data, we find that a good model is one which only includes the labeling index as a predictor:

  Coefficients
  Term Coef SE Coef 95% CI Z-Value P-Value VIF
  Constant -3.78 1.38 (-6.48, -1.08) -2.74 0.006
  LI 2.90 1.19 ( 0.57, 5.22) 2.44 0.015 1.00

  Regression Equation
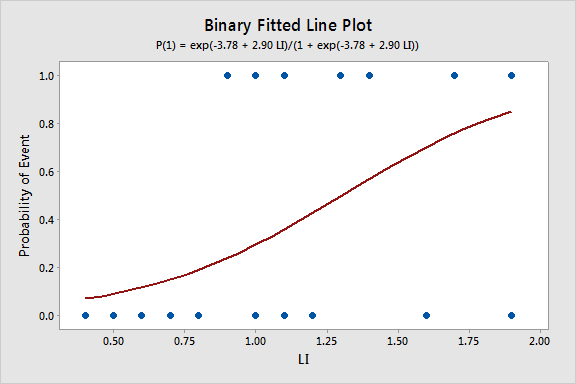
  P(1) = exp(Y')/(1 + exp(Y'))
  Y' = -3.78 + 2.90 LI

  Since we only have a single predictor in this model we can create a Binary Fitted Line Plot to visualize the sigmoidal shape of the fitted logistic regression curve:

  

  Odds, Log Odds, and Odds Ratio

  There are algebraically equivalent ways to write the logistic regression model:

  which is an equation that describes the odds of being in the current category of interest. By definition, the odds for an event is π / (1 - π) such that P is the probability of the event. For example, if you are at the racetrack and there is a 80% chance that a certain horse will win the race, then his odds are 0.80 / (1 - 0.80) = 4, or 4:1.

  which states that the (natural) logarithm of the odds is a linear function of the X variables (and is often called the log odds). This is also referred to as the logit transformation of the probability of success, \(\pi\).

  The odds ratio (which we will write as $\theta$) between the odds for two sets of predictors (say $\textbf_$ and $\textbf_$) is given by

  For binary logistic regression, the odds of success are:

  By plugging this into the formula for $\theta$ above and setting $\textbf_$ equal to $\textbf_$ except in one position (i.e., only one predictor differs by one unit), we can determine the relationship between that predictor and the response. The odds ratio can be any nonnegative number. An odds ratio of 1 serves as the baseline for comparison and indicates there is no association between the response and predictor. If the odds ratio is greater than 1, then the odds of success are higher for higher levels of a continuous predictor (or for the indicated level of a factor). In particular, the odds increase multiplicatively by $\exp(\beta_)$ for every one-unit increase in $\textbf_$. If the odds ratio is less than 1, then the odds of success are less for higher levels of a continuous predictor (or for the indicated level of a factor). Values farther from 1 represent stronger degrees of association.

  For example, when there is just a single predictor, \(X\), the odds of success are:

  If we increase \(X\) by one unit, the odds ratio is

  To illustrate, the relevant output from the leukemia example is:

  Odds Ratios for Continuous Predictors
  Odds Ratio 95% CI
  LI 18.1245 (1.7703, 185.5617)

  The regression parameter estimate for LI is $2.89726$, so the odds ratio for LI is calculated as $\exp(2.89726)=18.1245$. The 95% confidence interval is calculated as $\exp(2.89726\pm z_*1.19)$, where $z_=1.960$ is the $97.5^>$ percentile from the standard normal distribution. The interpretation of the odds ratio is that for every increase of 1 unit in LI, the estimated odds of leukemia remission are multiplied by 18.1245. However, since the LI appears to fall between 0 and 2, it may make more sense to say that for every 0.1 unit increase in L1, the estimated odds of remission are multiplied by $\exp(2.89726\times 0.1)=1.336$. Then

  • At LI=0.9, the estimated odds of leukemia remission is $\exp\=0.310$.
  • At LI=0.8, the estimated odds of leukemia remission is $\exp\=0.232$.
  • The resulting odds ratio is $\frac=1.336$, which is the ratio of the odds of remission when LI=0.9 compared to the odds when L1=0.8.

  Notice that $1.336\times 0.232=0.310$, which demonstrates the multiplicative effect by $\exp(0.1\hat>)$ on the odds.

  Likelihood Ratio (or Deviance) Test

  The likelihood ratio test is used to test the null hypothesis that any subset of the $\beta$'s is equal to 0. The number of $\beta$'s in the full model is k+1, while the number of $\beta$'s in the reduced model is r+1. (Remember the reduced model is the model that results when the $\beta$'s in the null hypothesis are set to 0.) Thus, the number of $\beta$'s being tested in the null hypothesis is \((k+1)-(r+1)=k-r\). Then the likelihood ratio test statistic is given by:

  where $\ell(\hat)$ is the log likelihood of the fitted (full) model and $\ell(\hat^)$ is the log likelihood of the (reduced) model specified by the null hypothesis evaluated at the maximum likelihood estimate of that reduced model. This test statistic has a $\chi^$ distribution with \(k-r\) degrees of freedom. Statistical software often presents results for this test in terms of "deviance," which is defined as \(-2\) times log-likelihood. The notation used for the test statistic is typically $G^2$ = deviance (reduced) – deviance (full).

  This test procedure is analagous to the general linear F test procedure for multiple linear regression. However, note that when testing a single coefficient, the Wald test and likelihood ratio test will not in general give identical results.

  To illustrate, the relevant software output from the leukemia example is:

  Deviance Table
  Source DF Adj Dev Adj Mean Chi-Square P-Value
  Regression 1 8.299 8.299 8.30 0.004
  LI 1 8.299 8.299 8.30 0.004
  Error 25 26.073 1.043
  Total 26 34.372

  Since there is only a single predictor for this example, this table simply provides information on the likelihood ratio test for LI (p-value of 0.004), which is similar but not identical to the earlier Wald test result (p-value of 0.015). The Deviance Table includes the following:

  • The null (reduced) model in this case has no predictors, so the fitted probabilities are simply the sample proportion of successes, \(9/27=0.333333\). The log-likelihood for the null model is \(\ell(\hat^)=-17.1859\), so the deviance for the null model is \(-2\times-17.1859=34.372\), which is shown in the "Total" row in the Deviance Table.
  • The log-likelihood for the fitted (full) model is \(\ell(\hat)=-13.0365\), so the deviance for the fitted model is \(-2\times-13.0365=26.073\), which is shown in the "Error" row in the Deviance Table.
  • The likelihood ratio test statistic is therefore \(\Lambda^=-2(-17.1859-(-13.0365))=8.299\), which is the same as \(G^2=34.372-26.073=8.299\).
  • The p-value comes from a $\chi^$ distribution with \(2-1=1\) degrees of freedom.

  When using the likelihood ratio (or deviance) test for more than one regression coefficient, we can first fit the "full" model to find deviance (full), which is shown in the "Error" row in the resulting full model Deviance Table. Then fit the "reduced" model (corresponding to the model that results if the null hypothesis is true) to find deviance (reduced), which is shown in the "Error" row in the resulting reduced model Deviance Table. For example, the relevant Deviance Tables for the Disease Outbreak example on pages 581-582 of Applied Linear Regression Models (4th ed) by Kutner et al are:

  Source DF Adj Dev Adj Mean Chi-Square P-Value
  Regression 9 28.322 3.14686 28.32 0.001
  Error 88 93.996 1.06813
  Total 97 122.318
  

  Source DF Adj Dev Adj Mean Chi-Square P-Value
  Regression 4 21.263 5.3159 21.26 0.000
  Error 93 101.054 1.0866
  Total 97 122.318
  

  Here the full model includes four single-factor predictor terms and five two-factor interaction terms, while the reduced model excludes the interaction terms. The test statistic for testing the interaction terms is \(G^2 = 101.054-93.996 = 7.058\), which is compared to a chi-square distribution with \(10-5=5\) degrees of freedom to find the p-value = 0.216 > 0.05 (meaning the interaction terms are not significant at a 5% significance level).

  Alternatively, select the corresponding predictor terms last in the full model and request the software to output Sequential (Type I) Deviances. Then add the corresponding Sequential Deviances in the resulting Deviance Table to calculate \(G^2\). For example, the relevant Deviance Table for the Disease Outbreak example is:

  Source DF Seq Dev Seq Mean Chi-Square P-Value
  Regression 9 28.322 3.1469 28.32 0.001
  Age 1 7.405 7.4050 7.40 0.007
  Middle 1 1.804 1.8040 1.80 0.179
  Lower 1 1.606 1.6064 1.61 0.205
  Sector 1 10.448 10.4481 10.45 0.001
  Age*Middle 1 4.570 4.5697 4.57 0.033
  Age*Lower 1 1.015 1.0152 1.02 0.314
  Age*Sector 1 1.120 1.1202 1.12 0.290
  Middle*Sector 1 0.000 0.0001 0.00 0.993
  Lower*Sector 1 0.353 0.3531 0.35 0.552
  Error 88 93.996 1.0681
  Total 97 122.318
  

  The test statistic for testing the interaction terms is \(G^2 = 4.570+1.015+1.120+0.000+0.353 = 7.058\), the same as in the first calculation.

  Goodness-of-Fit Tests

  Overall performance of the fitted model can be measured by several different goodness-of-fit tests. Two tests that require replicated data (multiple observations with the same values for all the predictors) are the Pearson chi-square goodness-of-fit test and the deviance goodness-of-fit test (analagous to the multiple linear regression lack-of-fit F-test). Both of these tests have statistics that are approximately chi-square distributed with c - k - 1 degrees of freedom, where c is the number of distinct combinations of the predictor variables. When a test is rejected, there is a statistically significant lack of fit. Otherwise, there is no evidence of lack of fit.

  By contrast, the Hosmer-Lemeshow goodness-of-fit test is useful for unreplicated datasets or for datasets that contain just a few replicated observations. For this test the observations are grouped based on their estimated probabilities. The resulting test statistic is approximately chi-square distributed with c - 2 degrees of freedom, where c is the number of groups (generally chosen to be between 5 and 10, depending on the sample size) .

  To illustrate, the relevant software output from the leukemia example is:

  Goodness-of-Fit Tests
  Test DF Chi-Square P-Value
  Deviance 25 26.07 0.404
  Pearson 25 23.93 0.523
  Hosmer-Lemeshow 7 6.87 0.442

  Since there is no replicated data for this example, the deviance and Pearson goodness-of-fit tests are invalid, so the first two rows of this table should be ignored. However, the Hosmer-Lemeshow test does not require replicated data so we can interpret its high p-value as indicating no evidence of lack-of-fit.

  R 2

  The calculation of R 2 used in linear regression does not extend directly to logistic regression. One version of R 2 used in logistic regression is defined as

  where $\ell(\hat>)$ is the log likelihood of the model when only the intercept is included and $\ell_(\beta)$ is the log likelihood of the saturated model (i.e., where a model is fit perfectly to the data). This R 2 does go from 0 to 1 with 1 being a perfect fit. With unreplicated data, $\ell_(\beta)=0$, so the formula simplifies to:

  To illustrate, the relevant software output from the leukemia example is:

  Model Summary
  Deviance Deviance
  R-Sq R-Sq(adj) AIC
  24.14% 21.23% 30.07

  Recall from above that \(\ell(\hat)=-13.0365\) and \(\ell(\hat^)=-17.1859\), so:

  Note that we can obtain the same result by simply using deviances instead of log-likelihoods since the $-2$ factor cancels out:

  Raw Residual

  The raw residual is the difference between the actual response and the estimated probability from the model. The formula for the raw residual is

  Pearson Residual

  The Pearson residual corrects for the unequal variance in the raw residuals by dividing by the standard deviation. The formula for the Pearson residuals is

  Deviance Residuals

  Deviance residuals are also popular because the sum of squares of these residuals is the deviance statistic. The formula for the deviance residual is

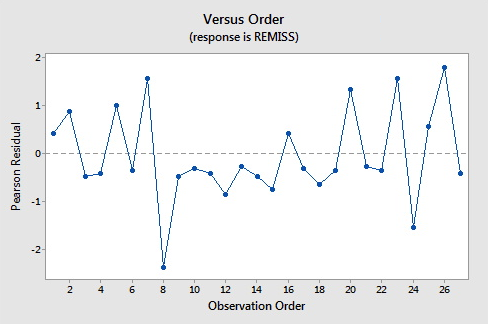
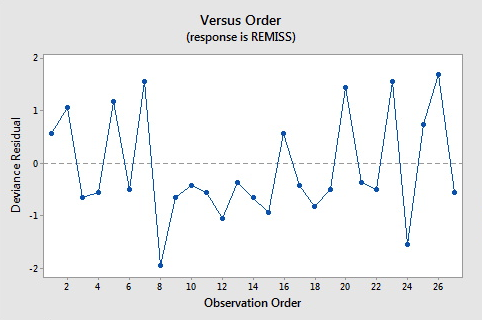
  Here are the plots of the Pearson residuals and deviance residuals for the leukemia example. There are no alarming patterns in these plots to suggest a major problem with the model.

  

  

  Hat Values

  The hat matrix serves a similar purpose as in the case of linear regression – to measure the influence of each observation on the overall fit of the model – but the interpretation is not as clear due to its more complicated form. The hat values (leverages) are given by

  where W is an $n\times n$ diagonal matrix with the values of $\hat<\pi>_(1-\hat<\pi>_)$ for $i=1 ,\ldots,n$ on the diagonal. As before, we should investigate any observations with $h_>3p/n$ or, failing this, any observations with $h_>2p/n$ and very isolated.

  Studentized Residuals

  We can also report Studentized versions of some of the earlier residuals. The Studentized Pearson residuals are given by

  and the Studentized deviance residuals are given by

  Cook's Distances

  An extension of Cook's distance for logistic regression measures the overall change in fitted logits due to deleting the $i^>$ observation. It is defined by:

  To illustrate, the relevant software output from the leukemia example is:

  Fits and Diagnostics for Unusual Observations
  Observed
  Obs Probability Fit SE Fit 95% CI Resid Std Resid Del Resid HI
  8 0.000 0.849 0.139 (0.403, 0.979) -1.945 -2.11 -2.19 0.149840
  Obs Cook’s D DFITS
  8 0.58 -1.08011 R
  R Large residual

  The residuals in this output are deviance residuals, so observation 8 has a deviance residual of \(-1.945\), a studentized deviance residual of \(-2.19\), a leverage (h) of \(0.149840\), and a Cook's distance (C) of 0.58.